Theory of computation

Theory of computation basics

• Symbol
  The symbol is the smallest building block in the theory of computation and can be any letter, number or even pictograms.
  For example: a, b, 0, 1
  
  
• Alphabet
  From the symbols we can form an alphabet represented by the sigma sign (Σ).
  The alphabet is nothing more than a collection of symbols (finite set).
  For example: Σ = {a,b}{0,1}
  
  
• String
  A string is a sequence of symbols from the alphabet.
  For example: Σ = {a,b}
  Possible strings are:
  • String "a" of length 1
  • String "b" of length 1
  • String "aa" of length 2
  • String "ab" of length 2
  • String "aaa" of length 3
  
  Question: How many strings of length 2 are possible over alphabet {a,b}?
  Answer: 4. The strings are: aa, ab, ba and bb
  
  Question: How many strings of length 2 and starting with "a" are possible over alphabet {a,b}?
  Answer: 2. The strings are: aa, ab
  
  Question: How many strings of length n are possible over alphabet {a,b}?
  Answer: 2ⁿ. Note: There are 2 symbols in the alphabet.
  
  Question: How many strings of length n are possible over alphabet {a,b,c,d}?
  Answer: |Σ|ⁿ = 4ⁿ. Note: There are 4 symbols in the alphabet.
  
  
• Language
  In general a language is a collection of words, but in the theory of computation a language is a collection of strings.
  For example: Σ = {a,b}
  
  L₁ = set of all strings of length 2.
  L₁ = {aa, ab, ba, bb}
  L₁ is called a finite language or a finite set.
  
  L₂ = set of all strings of length 3.
  L₂ = {aaa, aab, aba, abb, baa, bab, bba, bbb}
  L₂ is called a finite language or a finite set.
  
  L₃ = set of all strings where each string start with an "a".
  L₃ = {a, aa, ab, aaa, aab, aba, abb, ...}
  L₃ is called an infinite language or an infinite set.
  
  Note:
  A language which can be formed over an alphabet can be finite or infinite.
  
  
• Powers of Σ
  Σⁿ = Set of all strings over Σ of length n
  
  For example: Σ = {a,b}
  
  Σ⁰ = Set of all strings over Σ of length 0
  Σ⁰ = {ε}
  ε (epsilon) is a special symbol which represents an empty string "" with length 0.
  |ε| = 0
  |Σ⁰| = 0
  
  Σ¹ = Set of all strings over Σ of length 1
  Σ¹ = {a,b}
  |Σ¹| = 2
  
  Σ² = Set of all strings over Σ of length 2
  Σ² = Σ Σ = {a,b} {a,b} = {aa,ab,ba,bb}
  |Σ²| = 4
  
  Σ³ = Set of all strings over Σ of length 3
  Σ³ = Σ Σ Σ = {a,b} {a,b} {a,b} = {aaa,aab,aba,abb,baa,bab,bba,bbb}
  |Σ³| = 8
  
  
• Σ^*
  * means 0, 1, 2 ... n
  Σ^* = Σ⁰ ∪ Σ¹ ∪ Σ² ∪ ... Σⁿ
  Note: ∪ = union
  
  For example: Σ = {a,b}
  
  Σ^* = {ε} ∪ {a,b} ∪ {aa,ab,ba,bb} ∪ ...
  
  Σ^* = Set of all strings over Σ of ALL lengths.
  Σ^* represents an infinite set.
  Σ^* can be seen as the parent of all languages.
  
  L₁ ⊆ Σ^*
  L₂ ⊆ Σ^*
  L₃ ⊆ Σ^*
  
  Note: ⊆ = subset
  
  Question: How many languages are possible over Σ^*
  Answer: infinite
  
  
• How are strings and languages used in in practice.
  
  Question: Which symbols are used in the C programming language?
  Answer: Σ = {a,b..z,A,B..Z,0,1..9,+, * ...}
  The alphabet is finite.
  
  The program:
  
  void main(){
     int a,b
     :
  }
  
  is nothing more than a string.
  
  Question: What is the C programming language?
  Answer: Set of all valid programs.
  
  Question: How many programs are possible over the C programming language?
  Answer: infinite {P₁, P₂, P₃ ...}
  
  Question: If you have a program P_n how can you know if it valid?
  Answer: Check if the string (S) is available in the language (L). However the language is infinite, so you can not do this.
  
  Example:
  Σ = {a,b}
  
  L₁ = {aa, ab, ba, bb}
  Note: L₁ is finite.
  S = aa
  S is available in L
  
  L₂ = {a, aa, aaa, ab, ...}
  Note: L₂ is infinite.
  S = baba
  It takes forever to check if S is available in L
  
  To solve the last problem you must convert the language L to a finite representation F.
  
  
  
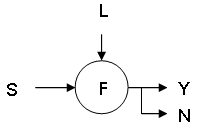
  The finite representation F can check if a string S is present in language L.
  If present the output is Y(es) otherwise the output is N(o).
  
  If the circle represents a machine with a finite amount of memory where the finite representation F is stored, the finite representation F is called the Finite Automata (FA).
  Note: An automata is a machine.
  
  
  
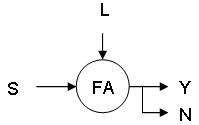
  There are two ways to create a finite representation of a language.
  For example: L₁ = Set of all strings which starts with an a.
  
  • Representation of a language using a finite set
    
    L₁ = {a,aa,ab,aaa,...}
    
    
  • Representation of a language using a Finite Automata (FA) diagram
    
    
    
    
    
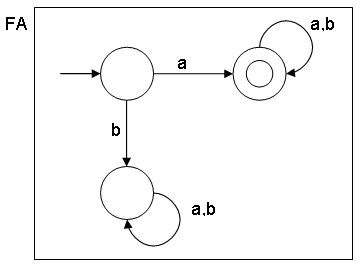
    • All circles are states.
    • A state represented by a circle with an "empty" arrow pointing to it is called the initial state.
      
      
      
      
    • A state represented by double circle is called the final state.
      
      
      
      
• How to read the Finite Automata diagram
  
  
  
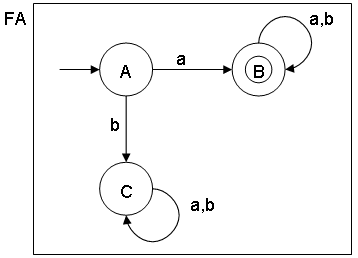
  For example:
  Language L₁ = {a,aa,ab,aaa...}
  String S = "aab"
  
  Question: Is string S present in language L₁, using the FA diagram?
  Answer: Scanning the entire string S we start with inital state A and ending with final state B:
  A -> a -> B -> a -> B -> b -> B
  Because we start with the inital state AND end with the final state, string S is present in language L₁.
  
  For example:
  Language L₁={a,aa,ab,aaa...}
  String S = "bba"
  
  Question: Is string S present in language L₁, using the FA diagram?
  Answer: Scanning the entire string S, we start with inital state A and ending with state C:
  A -> b -> C -> b -> C -> a -> C
  Because we start with the inital state AND do not end in the final state, string S is not present in language L₁.
  
  
• Finite Automata (FA) types
  Note: Automaton is singular, Automata is plural.
  
  
  
  
  
  
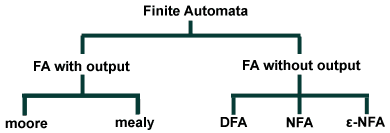
  DFA = Deterministic Finite Automata
  NFA = Non Deterministic Finite Automata
  ε-NFA = Non Deterministic Finite Automata with ε
  
  DFA (Deterministic Finite Automata)
  DFA is an automata which contains (Q, Σ, δ, q0, F)
  In general each finite automata can be represented by those 4 values.
  
  
  
  
  • Q is set of all states
    Q = {A,B,C}
  • Σ is set of all inputs
    Σ = {a,b}
  • q0 is the initial state
    q0 = A
  • F is set of all final states
    F = {B}
  
  Q ⊇ F (Q is a superset of F)
  
  The (Q, Σ, q0, F) are common for the DFA, NFA and ε-NFA the only difference is δ.
  
  δ = Q x Σ -> Q (This is called the transition function)
  
  For example (see also FA diagram above):
  Q = {A,B,C}
  Σ = {a,b}
  δ = {A,B,C} x {a,b} -> Q
  
  
  
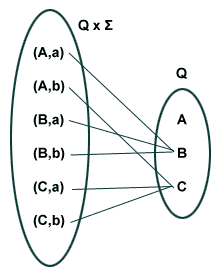
  According to the diagram:
  There is only one transition (line drawn) between (state A, input a) and state B.
  There is only one transition (line drawn) between (state A, input b) and state C.
  There is only one transition (line drawn) between (state B, input a) and state B.
  There is only one transition (line drawn) between (state B, input b) and state B.
  There is only one transition (line drawn) between (state C, input a) and state C.
  There is only one transition (line drawn) between (state C, input b) and state C.
  
  The definition of DFA:
  For every state, for every input there will be exactly 1 transition.
  This behaviour is important when creating compilers.